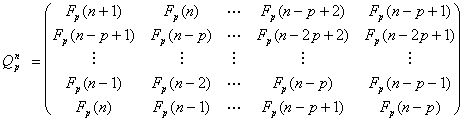| Математика Гармонии: история, теория, приложения | Ссылки: |
Спустя 2 500 лет после древних греков в современной науке на передний план вновь вышли те проблемы (счета, измерения и гармонии систем), которые были центральными проблемами античной науки и математики. Автору удалось объединить новые математические теории, созданные для решения этих проблем, в стройную математическую теорию, названную «Математикой Гармонии». В основе этой математики лежит «Золотое Сечение»! Эта новая математика может стать началом нового этапа в развитии «Высшей Математики» и основой для создания новой науки – «Науки о Гармонии Систем». Она может также стать началом реформы математического образования и новых компьютерных проектов, основанных на Золотом Сечении!
1. История «элементарной математики»
Как известно, математика условно может быть разделена на две части: элементарную и высшую. В русском языке словосочетание «Элементарная математика» в сравнении со словосочетанием «Высшая математика» носит некоторый уничижительный смысл. Оно звучит как нечто очень простое, «школьное», недостойное внимания «чистых математиков», высокое предназначение которых состоит в развитии «Высшей математики». Однако в английском языке словосочетание “Elementary mathematics” имеет совершенно другой смысл и означает “Fundamental mathematics”. Именно этот первоначальный смысл и заложен в английском названии одного из величайших математических сочинений – “Euclidean Elements” («Начала Евклида»). Таким образом, когда говорят об «элементарной математике», то это словосочетание надо понимать, как название той части математики, которая изучает исходные, первичные, фундаментальные понятия математики такие, как натуральное и иррациональное число, величина, арифметика, геометрия, тригонометрия, элементарные функции, то есть «элементарная математика» рассматривается как некоторый «математический фундамент», на котором и построено здание всей математики. Считается, что «элементарная математика» является наиболее устойчивой частью математики, и поэтому именно эта часть математики составляет основу современного математического образования. Это означает, что любые новые идеи в развитии «элементарной математики» имеют прямое отношение к математическому образованию.
Согласно мнению А.Н. Колмогорова период «элементарной математики» является одним из наиболее длительных периодов в истории математики: от древних греков до открытия логарифмов в начале 17 века. Если же к «периоду элементарной математики» добавить еще период предыстории математики (Вавилонская, Египетская, Китайская, Индусская математики), то речь идет о многотысячелетнем периоде в развитии математики, в течение которого и формировались и уточнялись исходные, начальные, фундаментальные математические идеи и понятия, которые в совокупности и составляют содержание «элементарной математики».
2. Теоретико-числовой фундамент «элементарной математики»
Подавляющее большинство математиков согласны с мнением, что в основе математики лежат следующие фундаментальные понятия – число, величина, функция – и что начальный период в развитии математики был направлен на развитие именно этих понятий. В этой области античными математиками были сделаны выдающиеся математические открытия, к которым, прежде всего, относятся:
2.1. Позиционный принцип представления чисел. Это математическое открытие было сделано вавилонскими математиками за 2000 лет до новой эры. Позиционный принцип лежит в основе десятичной системы, которую должен знать каждый ученик даже «церковно-приходской школы», а также двоичной системы, которая лежит в основе современных компьютеров. Ясно, что без позиционного принципа и десятичной системы был бы невозможен прогресс в развитии науки и технологии. Поэтому не случайно, что известный российский математик 19-го века академик М.В. Остроградский сравнил открытие позиционного принципа и основанной на нем десятичной системы с изобретением письменности по своему влиянию на развитие материальной культуры.
2.2. Создание тригонометрии. Тригонометрия на начальном этапе рассматривалась как прикладная математическая дисциплина, которая была создана для обслуживания потребностей астрономии и астрологии и была предназначена для вычисления координат планет на «сферических» орбитах. Именно тригонометрия дала математике тригонометрические функции, изучаемые в средней школе. Именно эти функции являются наиболее яркими представителями так называемых элементарных функций. Без тригонометрических функций немыслимо существование рядов Фурье, гармонического анализа и других поздних открытий математического анализа.
2.3. Формирование понятия натурального числа. Для изучения этого важнейшего математического понятия в античной математике сформировалась теория чисел, которая по праву называется царицей математики.
2.4. Открытие несоизмеримых отрезков, сделанное пифагорейцами, считается важнейшим математическим открытием в истории античной математики. Это открытие привело к первому кризису в основаниях математики, который завершился созданием теории измерения и теории иррациональных чисел.
2.5. Открытие логарифмов. Сделанное на завершающем этапе «периода элементарной математики», это открытие сыграло огромную роль в развитии математики и вычислительной техники. Это открытие значительно упростило практику математических вычислений, что способствовало бурному развитию астрономии и других наук. Вместе с логарифмами в математику были введены новые классы «элементарных функций» таких, как экспоненциальная, логарифмическая, гиперболические функции.
2.5. Фундаментальные математические константы p и е сыграли важную роль в математике, а выяснение их арифметической природы на многие столетия стало делом чести математиков. Однако особая роль этих чисел для математического анализа состоит в том, что именно они порождают главные классы «элементарных функций», в частности тригонометрические и гиперболические функции.
Существенно подчеркнуть, что на своем начальном этапе развитие математики стимулировалось вычислительной практикой. К разряду таких открытий, которые одновременно являются «фундаментальными» как для математики, так и для компьютерной техники относятся: позиционный принцип представления чисел, десятичная система, двоичная система, логарифмы и т.д.
С открытия дифференциального и интегрального исчислений, создателями которого являются гениальные математики Ньютон и Лейбниц, начинается период высшей математики; при этом на передний план в математике выходят новые проблемы, а проблемы «элементарной математики», которые лежали в основе античной математики, как бы отходят на второй план.
3. На пути к «Математике Гармонии»
Интересно подчеркнуть, что великие математики всегда понимали значение «элементарной математики» для развития всей математической науки. Гениальный русский геометр Н.И. Лобачевский как-то сказал: «Алгебру и Геометрию постигла одна и та же участь. За быстрыми успехами в начале следовали весьма медленные и оставили науку на такой ступени, где она еще далека от совершенства. Это произошло оттого, что Математики все свое внимание обратили на высшие части Аналитики, пренебрегая началами и не желая трудиться над обрабатыванием такого поля, которое они уже раз перешли и оставили за собою».
Во второй половине 20-го века в математике вновь возникает интерес к тем проблемам, которые традиционно относились к «элементарной математике». В связи с развитием информатики и компьютеров возникает новый интерес к проблеме систем счисления и новых компьютерных арифметик [1, 2], восходящий к вавилонской и египетской математикам.
Вторая проблема, к которой вновь возник интерес в современной науке, является проблема измерения, которая привела в античной науке к созданию геометрии. Д.И. Менделееву принадлежат замечательные слова «Наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры». В связи с «математизацией» науки насущной потребностью становится разработка общей теории измерения [3-6], которая и должна стать основой всех точных наук, так как все большее число наук (экономика, теория информация, социология, психология и др.) становятся «точными науками», а «измеряемыми» становятся «величины», которые до последнего времени считались «неизмеримыми»: информация, экономические показатели, эстетические ценности и т.д.
Еще одной тенденцией современных научных исследований является возврат к проблеме гармонии систем [7], которая стояла в центре античной науки; в связи с этим возникает интерес к знаменитому «Золотому Сечению», которое сыграло в развитии человеческой культуры не меньшую роль, чем число p, лежащее в основе тригонометрии. Иоганн Кеплер назвал Золотое Сечение одним из «сокровищ геометрии» и сравнил его со знаменитой «Теоремой Пифагора». Оценивая роль Золотого Сечения в развития древнегреческой культуры, гениальный российский философ Алексей Лосев как-то сказал: «С точки зрения Платона, да и вообще с точки зрения всей античной космологии, мир представляет собой некое пропорциональное целое, подчиняющееся закону гармонического деления – Золотого Сечения …».
«Гармонию Вселенной» (а именно эта проблема стояла в центре античной науки) с давних времен символизировали пять «правильных» геометрических тел, называемых «Платоновыми телами». Особую роль при этом играл додекаэдр – правильный 12-гранник, гранями которого являются правильные пятиугольники («пентаграммы»), основанные на Золотом Сечении. Отсюда следует, что число углов на поверхности додекаэдра равно 5x12=60 (что соответствует 60-летнему циклу). Додекаэдр имеет 30 ребер (что соответствует циклу Сатурна) и 12 граней (что соответствует циклу Юпитера), а произведение этих чисел 30x12=360. Следуя магической числовой символике додекаэдра, которая отражала числовую гармонию циклов Юпитера и Сатурна, древние вавилоняне и выбрали число 60 в качестве основания своей системы счисления, а древние египтяне пришли к мысли разбить год на 12 месяцев (число граней додекаэдра), каждый из которых содержал ровно 30 дней (число ребер додекаэдра). Таким и был египетский календарь, созданный в четвертом тысячелетии до н.э. В этом календаре год состоял из 365 дней. Он делился на 12 месяцев по 30 дней каждый, в конце года добавлялось пять праздничных дней, которые, однако, не входили в состав месяцев. Заметим, что в своей системе измерения времени и угловых величин египтяне также использовали «магические» числа додекаэдра (1 сутки = 24 (2x12) часа, 1 час = 60 минут, 1 минута = 60 секунд, 2p=360°, 1°=60').
С Золотым Сечением тесно связано другое математическое открытие, сделанное в 13-м веке выдающимся итальянским математиком Леонардо Пизано (по прозвищу Фибоначчи). Речь идет о так называемых числах Фибоначчи, которые были выбраны предметом математического исследования группой американских математиков, организовавшим в 1963 г. так называемую Фибоначчи-ассоциацию. Золотое Сечение и связанные с ними числа Фибоначчи пронизывает всю историю культуры. Пирамида Хеопса, скульптурные и архитектурные памятники греческой культуры и эпохи Ренессанса, непревзойденная «Джоконда» Леонардо да Винчи, картины Рафаэля, Шишкина и Константина Васильева, этюды Шопена, музыка Бетховена, Чайковского и Бэллы Барток, «Модулор» Корбюзье, сосновые шишки, кактусы, ананасы, морские звезды и раковины, Египетский календарь, квазикристаллы Шехтмана – вот далеко не полный перечень «произведений» Природы, Науки и Искусства, наполненных чудесной гармонией, в основе которой лежит Золотое Сечение!
Золотое Сечение занимают значительное место в современных исследованиях количественных соотношениях живой и неживой природы. Яркие открытия современной науки – квазикристаллы Шехтмана, новая геометрическая теория филлотаксиса украинского архитектора Боднара, закон структурной гармонии систем белорусского философа Сороко, резонансная теория Солнечной системы российского астронома Бутусова и другие современные научные открытия, основанные на Золотом Сечении, несомненно, имеют «стратегическое» значение для развития современной науки. Необходимо отметить также большой интерес современной теоретической физики к золотому сечению. Другими словами, в настоящее время невозможно представить себе дальнейшее развитие наук о природе без Золотого Сечения. И есть надежда, что и математическое образование также не останется в стороне от Золотого Сечения.
Таким образом, в современной науке созданы объективные предпосылки для возврата к тем проблемам (системы счисления, измерение, гармония систем), которые считались основными научными проблемами античной науки и привели к созданию «элементарной математики». Возникла «практическая необходимость» в развитии теории систем счисления, теории измерения и теории гармонии систем. И уже в первых книгах автора «Введение в алгоритмическую теорию измерения” [3] и «Коды золотой пропорции» [1] было показано, что все три научные проблемы античной математики (системы счисления, измерения и гармония систем) могут быть изложены в рамках единой математической теории, основанной на числах Фибоначчи и Золотом Сечении.
Впервые концепция создания новой математики, Математики Гармонии, основанной на золотом сечении, была изложена в докладе “The Golden Section and Modern Harmony Mathematics” [8], сделанном автором на 7-й Международной конференции «Числа Фибоначчи и их приложения» (Австрия, Грац, 1996 г.). В 1998 г. по инициативе академика Ю.А. Митропольского этот доклад был заслушан на заседании Украинского математического общества, результатом чего стала публикация статьи [9] в «Украинском математическом журнале».
Эта новая математика включает в себя следующие новые математические открытия, основанные на Золотом Сечении.
4. Обобщенный принцип Золотого Сечения
Пришедшая к нам из «Начал Евклида» задача о «делении отрезка в крайнем и среднем отношении», названная Леонардо да Винчи «золотым сечением», допускает следующее обобщение. Зададимся целым неотрицательным числом р (р=0, 1, 2, 3, …) и разделим отрезок АВ точкой С в таком отношении, чтобы
![]() . (1)
. (1)
Решение этой задачи привело к открытию нового класса иррациональных чисел tp (р=0, 1, 2, 3, ...), значения которых находятся в пределах: 1 GBP tp GBP 2. При этом числа tp являются корнями следующего алгебраического уравнения:
xp+1 = xp + 1. (2)
Заметим, что при р=0 число tp = 2, а деление отрезка в отношении (1) сводится к классической дихотомии. При р=1 число tp сводится к классическому «золотому сечению» ![]() . На этом основании числа tp были названы «обобщенными золотыми пропорциями» или «золотыми р-пропорциями», а деление отрезка в отношении (1) – «обобщенным золотым сечением» или «золотым р-сечением».
. На этом основании числа tp были названы «обобщенными золотыми пропорциями» или «золотыми р-пропорциями», а деление отрезка в отношении (1) – «обобщенным золотым сечением» или «золотым р-сечением».
«Золотые р-сечения» tp удовлетворяют следующему математическому тождеству, связывающему степени золотых р-пропорций:
![]() . (3)
. (3)
где n=0, ±1, ±2, ±3, … .
При n=0 тождество принимает следующий вид:
![]() . (4)
. (4)
откуда вытекает еще одно математическое тождество:
![]() , (5)
, (5)
которое выражает некоторый общий принцип разложения «Целого» («Единицы»), названного «обобщенным принципом золотого сечения».
Заметим, что этот общий принцип включает в себя в качестве частных случаев «Принцип дихотомии» (p=0) и классический «Принцип Золотого Сечения» (p=1), для которых общее тождество (5) принимает следующий вид соответственно:
«Принцип дихотомии» (p=0):
![]() (6)
(6)
«Принцип Золотого Сечения» (p=1):
![]() , (7)
, (7)
Исследуя так называемые «диагональные суммы» треугольника Паскаля, автор пришел к открытию новых рекуррентных последовательностей, названных обобщенными числами Фибоначчи или р-числами Фибоначчи, которые для заданного р (р=0, 1, 2, 3, ...) задаются с помощью следующей рекуррентной формулы:
Fp(n) = Fp(n-1)+Fp(n-p-1) для n>p+1; (8)
Fp(1) = Fp(2) = ... = Fp(p+1) = 1. (9)
Заметим, что рекуррентное соотношение (8) при начальных условиях (9) задает бесконечное количество новых числовых последовательностей. При этом их частными случаями являются «двоичный ряд» 1, 2, 4, 8, 16, …, соответствующий случаю р=0, и ряд Фибоначчи 1, 1, 2, 3, 5, 8, 13, …, соответствующий случаю р=1!
Легко доказать, что отношение соседних р-чисел Фибоначчи Fp(n)/Fp(n-1) при неограниченном увеличении n стремится к обобщенной золотой пропорции tp! Трудно переоценить методологическое значение этого математического результата, связывающего «обобщенный принцип золотого сечения», задаваемый (5), с треугольником Паскаля и биномиальными коэффициентами! Это может стать началом переосмысливания многих направлений современной математики и теоретической физики, основанных на комбинаторных отношениях, в частности, теории вероятностей и статистической физики.
5. Алгоритмическая теория измерения
Первой математической теорией, разработанной автором, в рамках проекта «Математики Гармонии», была «алгоритмическая теория измерения» [3-5]. Эта теория получила широкую известность и принесла автору славу одного из создателей современной «теоретической метрологии». Например, в одной из книг по теории измерения [10], написанной в развитие «алгоритмической теории измерения» [3-5], автор книги известный русский ученый П.А. Арутюнов в «Предисловии» приводит список ученых, внесших с его точки зрения наибольший вклад в развитии «Теории измерений». Имя автора в этом списке поставлено третьим после А.Н. Колмогорова и Н.В. Хованова. В 1980 г. брошюра «Алгоритмическая теория измерения» [4] была удостоена премии Министерства высшего и среднего образования УССР.
Популяризации «алгоритмической теории измерения» способствовали выступления автора на высоких научных форумах и собраниях. Огромный успех выпал на долю лекции «Алгоритмическая теория измерения и основания компьютерной арифметики», сделанной автором на объединенном заседании Компьютерного и Кибернетического обществ Австрии (Австрия, Вена, 1976). Именно эта лекция стала причиной начала широкого патентования изобретений автора в области «Компьютеров Фибоначчи» во всех ведущих странах-продуцентах компьютерной техники (США, Япония, Англия, Франция, Германия, Канада и др. страны).
6. Новое геометрическое определение действительного числа
В статье [9] автором предложен следующий подход к геометрическому определению действительного числа. Рассмотрим бесконечное множество геометрических отрезков, являющихся степенями золотой р-пропорции tp :
Gp ={ | (10) |
где р принимает значения из множества {0, 1, 2, 3, …}, а n – из множества {0, ±1, ±2, ±3, …}; при этом все степени ![]() связаны между собой математическим тождеством (3).
связаны между собой математическим тождеством (3).
Используя множество (10), можно «сконструировать» следующий метод позиционного представления действительных чисел:
![]() , (11)
, (11)
где aiI{0, 1}; tp (золотая р-пропорция) – основание позиционного представления (11); i = 0, ±1, ±2, ±3, … .
Заметим, что выражение (11) задает бесконечное количество позиционных способов представления чисел (систем счисления), так как каждому р (р=0, 1, 2, 3, …) соответствует своя система счисления типа (11). Заметим, что при р=0 основание tр = t0 = 2 и система счисления (11) сводится к классической двоичной системе счисления, лежащей в основе современных компьютеров.
Рассмотрим случай р=1. Для этого случая основанием системы счисления (11) является классическое «Золотое Сечение» t = ![]() и система (11) вырождается в «Тау-систему», введенную в 1957 г. американским математиком Джорджем Бергманом [11]. Бергман назвал свою «Тау-систему» системой счисления с иррациональным основанием. Любопытно отметить, что статья [11] написана Бергманом в возрасте 12 лет! Сейчас Джордж Бергман является профессором одного из американских университетов.
и система (11) вырождается в «Тау-систему», введенную в 1957 г. американским математиком Джорджем Бергманом [11]. Бергман назвал свою «Тау-систему» системой счисления с иррациональным основанием. Любопытно отметить, что статья [11] написана Бергманом в возрасте 12 лет! Сейчас Джордж Бергман является профессором одного из американских университетов.
Заметим также, что выражение (11) было введено автором в 1980 г. в статье [12] и названо кодом золотой р-пропорции. Теория этих систем счисления изложена в книге [1].
Рассмотрим теперь случай р=JPY. Для этого случая основание tр стремится к 1, а это означает, что в пределе выражение (11) сводится к классическому Евклидовому определению числа:
N = 1 + 1 + 1 + … + 1 (N раз). (12)
Как известно, «Евклидово определение» (12) порождает как сами натуральные числа, так и всю проблематику их теории. Но формула (11) задает бесконечное число новых определений действительного числа. Но тогда каждое из определений (11) «генерирует» свою собственную теорию действительных чисел! То есть теоретически существует бесконечное количество «теорий действительных чисел», основанных на определении (11)!
Коды золотой пропорции (11) стали основой новых компьютерных проектов, которые активно развивались в Таганрогском радиотехническом (1971-1977), в затем в Винницком политехническим институте (1997-1995) под научным руководством автора. Эти исследования вызвали широкий резонанс (не всегда положительный!) в советской компьютерной науке. В июне 1989 г. по инициативе Президента Академии наук Украины Б.Е. Патона доклад автора по «Компьютерам Фибоначчи» был заслушан на заседании Президиума Академии наук Украины. Одним из результатов доклада стала публикация статьи автора [2] в академическом журнале „Вісник Академії наук України”. Статья [2] была признана лучшей статьей журнала по итогам конкурса 1990 г.
7. Троичная зеркально-симметричная арифметика
Из последних результатов в этой области необходимо упомянуть о так называемой «Троичной зеркально-симметричной арифметике», разработанной автором несколько лет назад в период его работы профессором кафедры компьютерной техники Университета Аль Фатех (Ливия, Триполи, 1995-1997). «Троичная зеркально-симметричная система счисления» является синтезом системы счисления Бергмана [11] и троичной симметричной системы счисления, использованной Н.П. Брусенцовым при создании первого в истории науки троичного компьютера «Сетунь» (Московский университет). Новая компьютерная арифметика изложена автором в статье [13], опубликованной в международном журнале “The Computer Journal” (British Computer Society). Статья вызвала оживленный интерес западной компьютерной науки. Любопытно, что первым западным ученым, приславшим автору восторженное письмо по поводу новой компьютерной арифметике, оказался выдающийся американский ученый Дональд Кнут, автор всемирно известного научного бестселлера «Искусство программирования», переведенного на многие языки мира.
8. Гиперболические функции Фибоначчи и Люка
В 1993 г. автором совместно с И.С. Ткаченко был введен новый класс гиперболических функций, названных «Гиперболическими функциями Фибоначчи и Люка» [14]:
Фибоначчиевый гиперболический синус и косинус
| (13) |
Люковый гиперболический синус и косинус
| (14) |
Заметим, что для дискретных значений переменной x=k, k=0, ±1, ±2, ±3, …, фибоначчиевые и люковые гиперболические функции (13), (14) совпадают с числами Фибоначчи и числами Люка, причем
sF (k) = F2k; cF (k) = F2k+1; sL (k) = L2k+1; cL (k) = L2k. | (15) |
Свойство (15) является отличительной особенностью введенных выше гиперболических функций Фибоначчи и Люка (13), (15) по сравнению с классическими гиперболическими функциями (2), которые не имеют «дискретного аналога».
Функции (13), (14) обладают удивительными математическими свойствами. Приведем только некоторые из них:
![]() ;
; ![]() . (16)
. (16)
Дальнейшим развитием работы [14] являются так называемые «симметричные гиперболические функции Фибоначчи и Люка», изложенные в статье А.П. Стахова и Б.Н. Розина [15]. В 2003 г. автор опубликовал новую книгу [16], посвященную изложению теории новых гиперболических функций.
Что же дают гиперболические функции Фибоначчи и Люка для развития современной науки? Для ответа на этот вопрос обратимся еще раз к соотношениям (15). Из этих соотношений вытекает, что числа Фибоначчи и числа Люка являются частными («дискретными») случаями класса более сложных математических объектов, какими являются функции (13), (14). Например, в отличие от чисел Фибоначчи и Люка с функциями (13), (14) можно обращаться, как с обычными непрерывными функциями, то есть их можно интегрировать, дифференцировать и т.д. При этом каждому непрерывному тождеству для функций (13), (14) соответствует некоторое «дискретное» тождество для чисел Фибоначчи и Люка. Отсюда вытекает, что «теория чисел Фибоначчи» как бы «вырождается» и сводится к «теории гиперболических функций Фибоначчи и Люка». В таком неожиданном подходе и состоит первый «стратегический» научный результат, вытекающий из нового класса гиперболических функций, введенных в [14-16]. То есть математикам-фибоначчистам ничего не остается, как «сушить весла» и переходить к исследованию других математических объектов.
Украинский архитектор Олег Боднар, в своей книге [17] разработал новую геометрическую теорию ботанического явления «филлотаксиса», которое представляет собой одну из удивительных загадок живой природы. Моделируя рост филллотаксисных объектов (сосновых шишек, кактусов, ананасов, головок подсолнечника), он использовал гиперболические функции, подобные функциям (13), (14). Из исследований Боднара вытекает еще один «стратегический» вывод: возможно, что именно гиперболические функции Фибоначчи и Люка, обладающие «гиперболическими» и «рекуррентными» свойствами, лежит в основе неевклидовой геометрии живой природы.
Выше мы упоминали, что гиперболические функции лежат в основе «геометрии Лобачевского» и «четырехмерного мира Минковского». Но функции (13), (14) вполне можно использовать для разработки «гиперболической геометрии Лобачевского-Фибоначчи» и «четырехмерного мира Минковского-Фибоначчи»! Трудно переоценить значение такого подхода для развития современных космологических исследований!
9. Матрицы Фибоначчи, «золотые» матрицы и новая теория кодирования
Еще одним математическим достижением автора, полученным в рамках «Математики Гармонии», является разработка теории матриц особого типа, обладающих исключительными математическими свойствами. В статье [18] изложена теория квадратных матриц, названных Qp-матрицами Фибоначчи.
Если задаться некоторым целым р (р=0, 1, 2, 3, ....), то матрица Qp может быть представлена в виде следующей квадратной матрицы размером (р+1)x(р+1):
| (17) |
Заметим, что Qp-матрица представляет собой квадратную матрицу размером (p+1)x(p+1). Как вытекает из (17), она содержит в себе единичную матрицу размером (pxp), ограниченную последней строкой, состоящей из нулей, и первым столбцом, который состоит из нулей, ограниченных единицами. Для случаев p = 0, 1, 2, 3, 4 Qp-матрицы имеют следующий вид соответственно
Q0 = (1) ; ![]() ;
; 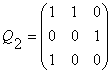 ;
;
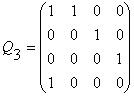 ;
; 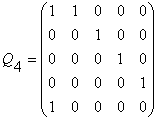 .
.
Матрицы Qp связаны друг с другом следующими простыми соотношениями. Если в матрице Q4 вычеркнуть последний столбец и предпоследнюю строку, то она вырождается в матрицу Q3 . Вычеркнув теперь последний столбец и предпоследнюю строку в матрице Q3, мы получим матрицу Q2 и т.д. Таким образом, каждая матрица Qp, с одной стороны, содержит в себе все предыдущие матрицы и, с другой стороны, входит во все последующие матрицы. Эта удивительная регулярность в построении матриц Qp вызывает неосознанное чувство ритма и гармонии!
Заметим, что для случая р=1 Qp-матрица (17) сводится к классической Q-матрице
![]() , (18)
, (18)
теория которой была разработана математиками-фибоначчистами во главе с Вернером Хогаттом, создателем Фибоначчи-ассоциации (США) [19].
Доказаны следующие теоремы для степеней Qp-матрицы [18].
Теорема 1. Для заданного целого р (р = 1, 2, 3, …) и заданного целого n (n = 0, ±1, ±2, ±3, …) имеет место следующее выражение для n-й степени матрицы Qp :
| (19) |
Теорема 2.
Det ![]() = (-1)pn, (20)
= (-1)pn, (20)
где p = 0, 1, 2, 3, … ; n = 0, ±1, ±2, ±3, … .
И теперь мы можем выразить наше восхищение по поводу Теорем 1 и 2. Действительно, невозможно вообразить, что p-числа Фибоначчи (8), (9), полученные автором при исследовании треугольника Паскаля, могут стать основой нового класса квадратных матриц, задаваемых выражениями (17) и (19). Но результат (20) кажется совершенно невероятным для специалистов, знакомых с понятием детерминанта матрицы! Невозможно вообразить, чтобы для любых заданных р и n детерминант любой матрицы (20) (а число таких матриц бесконечно!) всегда будет равен либо 1, либо (-1), что непосредственно следует из (20)! Ясно, что тождество (20) для матрицы (19) представляют нам неограниченные возможности для «фибоначчиевых» исследований и позволяют получить бесконечное число фундаментальных тождеств, связывающих p-числа Фибоначчи Fp(n) с биномиальными коэффициентами и треугольником Паскаля. Таким образом, если американский математик Вернер Хоггат исследовал только одну матрицу типа (18), которая стала для него источником новых идей в развитии теории чисел Фибоначчи, то невозможно вообразить, сколько новых научных результатов может принести исследование матриц (17), (19)!
Еще один необычный класс квадратных матриц, названных «золотыми» матрицами, разработан автором совсем недавно [20]. Рассмотрим пример «золотой» матрицы:
![]() (21)
(21)
Заметим, что элементами матрицы (21) являются гиперболические функции Фибоначчи (13). Заметим, что матрица (21) является функцией непрерывной переменной x, которая изменяется в пределах от -JPY до +JPY, то есть выражение (21) на самом деле задает бесконечное число квадратных матриц, множество которых совпадает с множеством действительных чисел! Но самым удивительным является следующий результат, основанный на тождествах (16). Доказано [20], что детерминант матрицы (21) не зависит от переменной x и всегда тождественно равен 1!
Какое же практическое приложение могут иметь матрицы (17), (19), (21)? В работах автора [20, 21] разработана новая теория кодирования, которая может быть эффективно использована для обнаружения и исправления ошибок в «каналах связи», а также для криптографической защиты информации. Учитывая высокую ошибкообнаруживающую и криптографическую способность метода и простоту его технической и программной реализации, можно ожидать, что метод найдет широкое применение в таких важных системах связи, как военные и космические системы связи, банковские системы связи, Интернет, телефонные и радио системы связи и др.
10. Заключение
Таким образом, автор берет на себя смелость утверждать, что исследования автора, изложенные в работах [1-9, 12-22], привели к созданию новой математики, названной автором «Математикой Гармонии» [8]. «Математика Гармонии» в своих истоках восходит к «пифагорейской математике» и является дополнением и развитием классической «Элементарной Математики», лежащей в основе современного математического образования. «Математика Гармонии» предлагает новый математический аппарат, который может быть эффективно использован для моделирования тех процессов объективного мира, где «Золотое Сечение» и числа Фибоначчи являются сутью того или иного физического или биологического явления (квазикристаллы, деление биологических клеток, филлотаксис и др.).
«Сердцем» новой математики является «Обобщенный Принцип Золотого Сечения», вытекающий из Треугольника Паскаля, «Алгоритмическая теория измерения», «Новая теория чисел», основанная на обобщенных золотых сечениях, «Гиперболические функции Фибоначчи и Люка», «Матрицы Фибоначчи», «Золотые» матрицы» и др.
Алгоритмическая теория измерения генерирует бесконечное число новых числовых последовательностей, в частности, p-числа Фибоначчи, биномиальные коэффициенты, последовательности двоичных и натуральных чисел. Эти числовые последовательности приводят к расширению «теории чисел Фибоначчи». Алгоритмическая теория измерения приводит также к развитию позиционных систем счисления, восходящих к Вавилонской шестидесятеричной системе счисления. Благодаря такому подходу этот «старейший» раздел теории чисел превращается в оригинальную математическую теорию, являющуюся дополнением к классической теоретической арифметике.
Как упоминалось выше, обнаруженная выше связь «Обобщенного Принципа Золотого Сечения» с Треугольником Паскаля может иметь «стратегическое» значение для современного теоретического естествознания. Она может стать началом переосмысливания многих направлений современной математики и теоретической физики, основанных на комбинаторных отношениях, в частности, теории вероятностей и многих статистических законов.
Формулы Бине, введенные в 19 в. французским математиком Бине, «генерируют» новый класс элементарных функций, гиперболические функции Фибоначчи и Люка [14-16]. Эти функции являются ничем иным, как обобщением формул Бине на «непрерывную» область. Благодаря этим функциям «теория чисел Фибоначчи» превращается в «непрерывную» теорию, потому что каждое математическое соотношение для функций Фибоначчи и Люка имеет дискретный аналог в рамках «теории чисел Фибоначчи». Новый класс гиперболических функций, обладающих рекуррентными свойствами, имеет «стратегическое» значение для развития биологии и теоретической физики, если учесть ту роль, которую гиперболические функции играют в современной теоретической физике («гиперболическая геометрия Лобачевского», «четырехмерный мир Минковского» и т.д.). Гиперболические функции Фибоначчи и Люка являются основой для новой геометрии филлотаксиса (геометрии Боднара) [17], которая является блестящим подтверждением эффективности гиперболических функций Фибоначчи и Люка для моделирования биологических процессов.
Широко известно следующее высказывание Иоганна Кеплера: «В геометрии существует два сокровища – теорема Пифагора и деление отрезка в крайнем и среднем отношении. Первое можно сравнить с ценностью золота, второе можно назвать драгоценным камнем».
К сожалению, приходится констатировать, что в современном математическом образовании роль «Золотого Сечения» незаслуженно принижена. В чем причина этого? Возможно, причина состоит в широком использовании «Золотого Сечения» в астрологии и так называемых «эзотерических науках». Известно, что основные символы астрологии (астра, пентаграмма, Платоновы тела и т.д.) тесно связаны с «Золотым Сечением». Возможно, что именно это обстоятельство и стало основной причиной того, что «материалистическая» наука, а вместе с ней и «материалистическое» образование выбросили «Золотое Сечение» на «свалку сомнительных научных концепций» и тем самым «кастрировали» современное математическое образование. Результат налицо: большинство так называемых «образованных» людей знают «Теорему Пифагора», но при этом имеют весьма смутное представление о золотом сечении, «втором сокровище геометрии» (Иоганн Кеплер). Ясно, что введение «Математики Гармонии» в современное математическое образование стало бы важным событием в образовании, что значительно повысило бы интерес учащихся к математике и способствовало бы повышению интереса учащихся к Искусству и наукам о Природе, где «Золотое Сечение» играет основополагающую роль.
Наконец, «Коды Фибоначчи», «Коды Золотой Пропорции», «Матрицы Фибоначчи» и «Золотые матрицы», разработанные в рамках «Математики Гармонии», могут стать источником новых идей в развитии компьютеров и коммуникационных систем.
Интерес к числам Фибоначчи и золотому сечению и проблемам гармонии систем, возникший в современной науке, является отражением «естественного» хода развития современной науки, которая приближается к раскрытию законов гармонии, созданию новой научной картины мира, основанной на идеях гармонии, симметрии и золотого сечения. Это приведет к восстановлению и углублению связей между Наукой и Искусством как двух взаимно дополняющих друг друга методов раскрытия и отображения объективной гармонии Мироздания. Для решения этих проблем в современной науке должна возникнуть новая интегральная наука, называемая «Наукой о Гармонии Систем» [7, 22], в которой числа Фибоначчи и золотое сечение должны занимать достойное место.
Литература:
1. Стахов А.П. Коды золотой пропорции. - Москва: Радио и связь, 1984
2. Стахов О.П. За принципом золотої пропорції: перспективний шлях розвитку обчислювальної техніки. Журнал "Вісник Академії наук Української РСР", №1-2, 1990 г.
3. Стахов А.П. Введение в алгоритмическую теорию измерения. - Москва: Советское Радио, 1977.
4. Стахов А.П. Алгоритмическая теория измерения. – Москва: Знание, 1979.
5. Stakhov A.P. The Golden Section in the Measurement Theory. An International Journal "Computers & Mathematics with Applications", Volume 17, No 4-6, 1989.
6. Стахов О.П. Вимірювання - фундаментальна проблема науки. Журнал "Вісник Академії наук Української РСР", №6, 1991 г.
7. Стахов О.П. Золотий переріз і наука про гармонію систем. Журнал "Вісник Академії наук Української РСР", №12, 1991 г.
8. Stakhov A.P. The Golden Section and Modern Harmony Mathematics. Applications of Fibonacci Numbers, 1998, V. 7.
9. Стахов А.П. Обобщенные золотые сечения и новый подход к геометрическому определению числа. Украинский математический журнал, 2004, т. 56, №8.
10. Арутюнов П.А. Теория и применение алгоритмических измерений. – Москва: Энергоатомиздат, 1990.
11. Bergman, G. A number system with an irrational base. Mathematics Magazine, No 31, 1957.
12. Стахов А.П. «Золотая» пропорция в цифровой технике. - Автоматика и вычислительная техника, 1980, №1.
13. Stakhov A.P. Brousentsov’s Ternary Principle, Bergman’s Number System and Ternary Mirror-symmetrical Arithmetic. - The Computer Journal (British Computer Society), Vol. 45, No 2.
14. Стахов А.П., Ткаченко И.С. Гиперболическая тригонометрия Фибоначчи. – Доповіді Академії наук Україны, 1993, №7.
15. Stakhov A., Rozin B. On a new class of hyperbolic function. - Chaos, Solitons & Fractals, 2004, V. 23, No.2. – pp. 379-389.
16. Stakhov A.P. Hyperbolic Fibonacci and Lucas functions: A new mathematics for the alive nature. - Vinnitsa, Publisher “ITI”, 2003.
17. Боднар О.Я. Золотое сечение и неевклидова геометрия в природе и искусстве. – Львов: Издательство «Свит», 1994.
18. Stakhov O.P. A generalization of the Fibonacci Q-matrix. - Доповіді Національної Академії наук України. 1999, № 9.
19. Hoggat Verner E. Fibonacci and Lucas Numbers. - Palo Alto - Houghton-Mifflin, 1969.
20. Stakhov A.P. Fibonacci Computer Science (manuscript). - Toronto, Bolton, 2004.
21. Stakhov A.P., Massingua V., Sluchenkova A.A. Introduction into Fibonacci Coding and Cryptography. - Kharkov: Publisher “Osnova” of Kharkov State University, 1999.
22. Стахов А.П. Священная геометрия и математика гармонии. Сборник трудов Винницкого аграрного университета «Проблемы Гармонии, Симметрии и Золотого Сечения в Природе, Науке и Искусстве», Издательство Винницкого аграрного университета, 2003, вып. 15.
http://www.obretenie.info/txt/stahov/delfus.htm
 Автор:
Автор: